Nie robimy żadnego błędu. Obliczamy odcinek pomiędzy punktami upadku ziarna i podajnika. Na sztywnej żyłce. Reszta wynikać będzie z warunków na łowisku. Wiatru, ciężaru podajnika, grubości żyłki, oporu stawianego jej przez wodę (zależy od ilości syfu na powierzchni np.).
W całym tym zadaniu chodzi o to, żeby wiedzieć, że ta odległość jest znikoma i nie trzeba sobie nią zaprzątać głowy. Trzeba tylko sprawdzić, jaką długość żyłki po zarzuceniu zwiniemy, by napiąć szczytówkę. Np. licząc obroty korbką kołowrotka i mnożąc przez jego nawój. Jeśli nam wyjdą dwa obroty, a kołowrotek ma nawój 80 cm. To mamy albo dodać ten 1,60 m na klipie, albo przy spombowaniu o tę odległość się cofnąć. I tyle. Nie musimy więc brać pod uwagę nieznanej nam odległości wynikającej z twierdzenia Pitagorasa. Bo ona nie ma znaczenia.
I nie robimy żadnego błędu.
Z całym szacunkiem dla Twojej pracy w zalinkowanym wątku 
, to nie ma potrzeby tworzyć jakichś wymyślnych wzorów, w których zawrzemy opór wody i prędkość wiatru - zmiennych, które za każdym razem będą inne i nie da się ich przewidzieć. Wystarczy policzyć obroty korbką na kołowrotku.
Odległość ta może być znikoma, ale może też wynosić pojedyncze metry w zależności od głębokości oraz długości żyłki i tej odległości nie pomierzymy kołowrotkiem.
Właśnie dlatego powstał artykuł
https://splawikigrunt.pl/forum/index.php?topic=1503.msg478141#msg478141 aby mieć rozeznanie co dzieje się pod wodą i z jakimi odległościami podajnika od zanęconego miejsca przy opadzie na napiętej żyłce możemy mieć do czynienia w praktyce. Obliczenia są proste i bazują na wzorze Pitagorasa.
Wracając do meritum sporu, czyli czyj wzór na odległość pomiędzy ziarnem ze spomba i podajnikiem jest prawidłowy, podaję z czego mój wzór wynika.
Twój wzór jest nieprawidłowy.
Poniżej mamy rysunek sytuacyjny opadu podajnika.
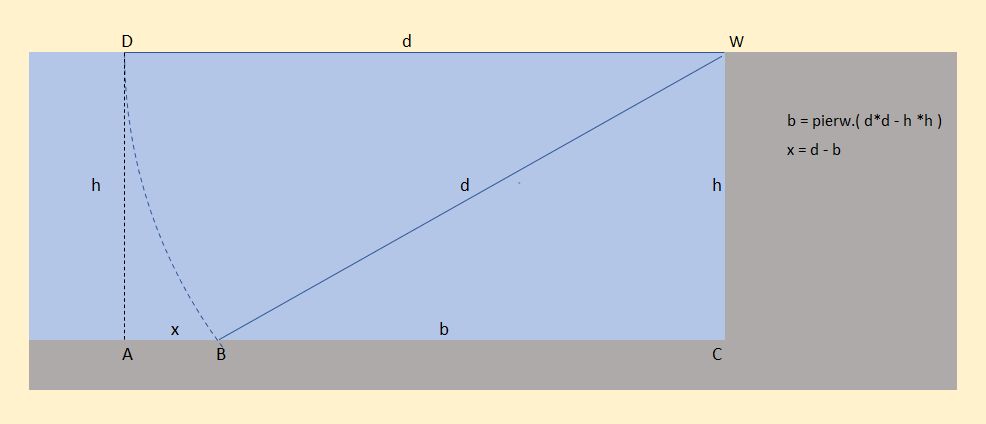
Opad podajnika na napiętej żyłce.
Założenia:
Długość żyłki spomb-klips jest taka sama jak podajnik-klips i na rysunku wynosi d.
W momencie kiedy spomb i podajnik dotykają wody w punkcie D żyłka jest wyprostowana.
Żyłka podczas opadu podajnika w wodzie jest cały czas napięta co skutkuje tym, że podajnik opada po łuku DB i zbliża się do brzegu.
Nie bierzemy pod uwagę oporów ruchu żyłki w wodzie, co skutkuje tym, że łuk opadu podajnika jest wycinkiem okręgu, a żyłka w czasie opadu nie wybrzusza się i jest odcinkiem prostym.
X = AB, b = BC, d = DW = BW, h = AD = CW
ZarzucaniePoczątek żyłki jest w punkcie W (szczytówka).
Zarzucony spomb wpada na prostej żyłce do wody w punkcie D, a jego ziarno opada na dno do punktu A.
Zarzucony podajnik wpada do wody na prostej żyłce także w punkcie D, a następnie opada po łuku okręgu do punktu B na dnie. Środkiem tego okręgu jest punkt W.
Ze wzoru Pitagorasa:
b = pierwiastek ( d*d -b*b )
Długość odcinka x pomiędzy ziarnem i podajnikiem wynosi więc:
x= d – b
Czyli:
x = d – pierwiastek ( d*d -h*h ) W rzeczywistości odcinek ten jest dodatkowo powiększony wybrzuszeniem opadającej w wodzie żyłki. Luz żyłki spowodowany tym wybrzuszeniem można zmierzyć licząc obroty korbką kołowrotka po opadnięciu podajnika.
Wielokrotnie mierzyłem ten luz na dystansie ok. 25 m oraz głębokości 4,5 m. Praktycznie wynosił ok.1,5-2 m w zależności od przykładanej staranności.
Odległość ziarno-podajnik x wynikająca z powyższego wzoru w praktyce może zawierać się w granicach od pojedynczych centymetrów dla dużych odległości zarzucania do nawet kilku metrów przy małych długościach żyłki i dużych głębokościach.
Przykładowo dla d = 30 m i h = 2 m x wynosi 6,7 cm, dla d = 30 m i h = 8 m x = 1,1 m, a dla d = 14 m i h = 8 m x = 2,5 m.
Odległości x pomiędzy ziarnem i podajnikiem rosną wraz z podniesioną szczytówki wędziska w czasie opadu zestawu w wodzie.
Wzór podany przez Michała jest nieprawidłowy dlatego, że bazuje na założeniu równości przeciwprostokątnej AW ( nie ma jej narysowanej na rysunku) z sumą x + d, a takiej równości nie ma. Odcinek AW jest zawsze krótszy od tej sumy niezależnie od głębokości h i odległości d i jego obliczanie nie jest potrzebne do wyznaczenia odległości ziarno-podajnik.
